引入
先问几个问题。
什么是树状数组？
树状数组是一种数据结构，支持 \(\log\) 级别的区间修改查询操作。
为什么要有树状数组？
用数组实现区间查询、区间修改是 \(O(n)\) 的，但用树状数组是 \(O(\log n)\)。
线段树和树状数组的对比？
名字不一样- 两个都是 \(\log\) 级数据结构
- 树状数组支持区间查询，区间修改，但线段树支持基本上所有区间操作（\(\log n\) 时间）
- 树状数组空间复杂度 \(n\)，常数小；线段树空间复杂度 \(4n\)，常数较大。
树状数组原理介绍
前置芝士
位运算
大意： 按位与：在二进制中对每一位进行对应操作：1&1=1, 1&0=0, 0&1=0, 0&0=0
二叉树
大意： 二叉树的定义：每个节点至多有 2 个儿子的树。
树状数组原理
首先上一张二叉树的图：（为了方便将节点右对齐）
图片来源：https://www.cnblogs.com/xenny/p/9739600.html，已经过博主同意，下同。
![]( "线段树")
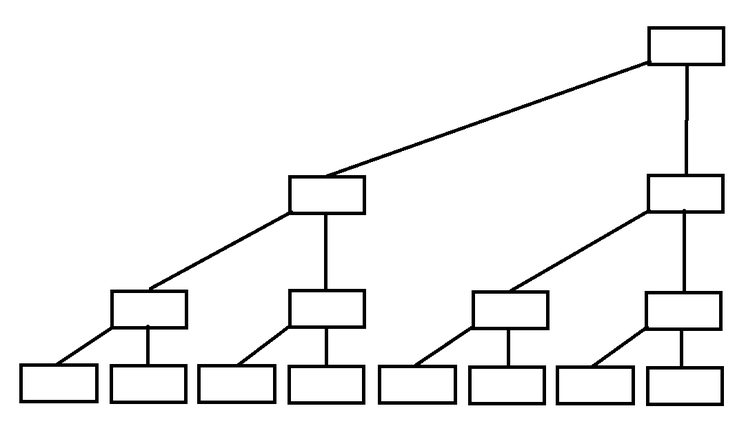
是不是看着有些熟悉呢？没错，这就是线段树。
但是树状数组可不长这样，前面说过它的空间复杂度是 \(n\)。
那树状数组是什么样呢？我们将每一列都只留最上面的节点，就变成了这样：
![]( "树状数组")
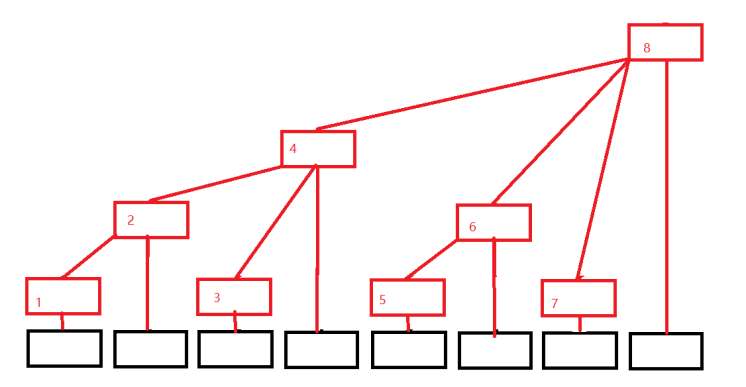
我们发现：（设原数组是 a[]，树状数组是 c[]）
1
2
3
4
5
6
7
8
| c[1] = a[1]
c[2] = a[1] + a[2]
c[3] = a[3]
c[4] = a[1] + a[2] + a[3] + a[4]
c[5] = a[5]
c[6] = a[5] + a[6]
c[7] = a[7]
c[8] = a[1] + a[2] + a[3] + a[4] + a[5] + a[6] + a[7] + a[8]
|
找规律发现：\(c[i] = \sum_{j = i - lowbit(i) + 1}^i a_j\)
关于 \(lowbit\)
\(lowbit(i)\) 表示 \(i\) 在二进制下最后一个 \(1\)。
例如：（下面的数都是二进制下的）
1
2
3
4
5
6
| lowbit(1111) = 1
lowbit(1100) = 100
lowbit(1010) = 10
lowbit(1001) = 1
lowbit(1000) = 1000
...
|
那么这个 \(lowbit\) 怎么求呢？
不难发现有很多求法，例如：
1
2
3
| x = 1001010
~x = 0110101
~x + 1 = 0110110
|
容易发现 x 与 ~x + 1 除了 \(lowbit\) 位相同，其它的都不同（显然）。 所以我们得出 lowbit(i) = x & ((~x) + 1)，然后因为 (~x) + 1 就是 -x（参见原码补码反码详解或这个），所以 lowbit(x) = x & -x。
于是我们成功处理了 \(lowbit\)！
应用
说了这么多，树状数组到底是怎么维护区间的呢？
维护区间有四种，分别是：
- 单点修改，单点查询
- 单点修改，区间查询
- 区间修改，单点查询
- 区间修改，区间查询
下面来分别讲解。
单点修改，单点查询
传统数组即可。
单点修改，区间查询
![]( "树状数组")
查询
从上图中我们发现 \[ \sum_{i = 1}^k a_i = c(i) + c(i - lowbit(i)) + c(i - lowbit(i) - lowbit\left(i - lowbit(i)\right) + \cdots + c(1) \]
证明
\[\begin{aligned} c(i) = &\sum_{k = i - lowbit(i) + 1}^i a_k\\ c(i - lowbit(i)) = &\sum_{k = i - lowbit(i) - lowbit(i - lowbit(i)) + 1}^{i - lowbit(i)} a_k\\ &\vdots\\ a(1) = &a_1 \end{aligned}\]
上初步代码：
1
2
3
4
5
6
7
8
| int query(int r) {
int ret = 0;
while(r > 0) {
ret += c[r];
r -= lowbit(r);
}
}
|
还有一个问题，如果 \(r = 0\) 呢？
此时我们求的是 \(a[0 .. r]\) 的和，但我们的条件是 r > 0 啊！
这时我们需要特殊处理 \(0\)。
为什么别的模板有些没有这么做呢？因为他们没有用到 a[0]。
模板：
1
2
3
4
5
6
7
8
9
10
| int query_sum(int r) {
if(r == 0) return c[0];
int ret = 0;
while(r) ret += c[r], r -= (r & -r);
return ret + c[0];
}
int query_sum(int l, int r) {
if(l == 0) return query_sum(r);
return query_sum(r) - query_sum(l - 1);
}
|
修改
修改时我们需要将包含 \(a_i\) 的 \(c\) 都修改，即：
\(c(i)\), \(c(i + lowbit(i))\), \(c(i + lowbit(i) + lowbit(i + lowbit(i)))\), \(\cdots\)
代码：
1
2
3
4
| void modify_add(int x, int y) {
if(x == 0) { t[x] += y; return; }
while(x <= tot) c[x] += y, x += (x & -x);
}
|
其中 tot 为树状数组下标的最大值。
区间修改，单点查询
前置芝士
差分数组
大意：
设 \(t(i) = a_i - a_{i - 1}\)
那么 \(a_i = \sum_{j = 1}^i t(j)\)
原理
树状数组可以维护单点修改，区间查询，但如何实现区间修改，单点查询呢？
我们可以用维护 \(a\) 的差分数组，而不是 \(a\) 数组。
此时区间修改 \([l, r]\) 可以转化成 a[l] += add, a[r + 1] -= add，即单点修改；
单点查询 \(a_x\) 可以转化成询问 \([1, x]\) 的和，即区间查询。
区间修改，区间查询
仍然利用差分：\(t(i) = a_i - a_{i - 1}\)
查询
\[\begin{aligned} \sum_{i = 1}^k a_i &= (t(1)) + (t(1) + t(2)) + (t(1) + t(2) + t(3)) + \cdots + \sum_{i = 1}^k t(i)\\ &= \sum_{i = 1}^k \sum_{j = 1}^i t(j)\\ &= \sum_{j = 1}^k \sum_{i = j}^k t(j)\\ &= \sum_{j = 1}^k t(j) \times (k - j + 1)\\ &= (k + 1) \sum_{j = 1}^k t(j) - \sum_{j = 1}^k t(j) \times j \end{aligned}\]
维护两个树状数组，一个 \(t(i)\)，一个 \(t(i) \times i\)。
修改
第一个 \(t(i)\) 的树状数组可以像最开始一样维护，下面考虑如何维护第二个 \(t(i) \times i\) 的树状数组。
在 a[l .. r] += k 时，\(t(l + 1 .. r)\) 是不会变的，所以 \(t(j) \times j (l < j \le r)\) 也都不会变。
那么对于 \(l\)，\(t(l)\) 增加了 \(k\)，则 \(t(l) \times l\) 增加了 \(k \times l\)；\(t(r + 1)\) 减少了 \(k\)，则 \(t(r + 1) \times (r + 1)\) 减少了 \(k \times (r + 1)\)。
总结一下就是 t[l] += l * k, t[r + 1] -= (r + 1) * k。
代码见模板。
模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| typedef long long LL;
const int N = ;
const int MOD = ;
struct BIT {
int tot;
struct {
int c[N];
int query_sum(int r) {
if(r == 0) return c[0];
LL ret = 0;
while(r) ret = (ret + c[r]) % MOD, r -= (r & -r);
return (ret + c[0]) % MOD;
}
void modify_add(int x, int y) {
if(x == 0) { c[x] = (c[x] + y) % MOD; return; }
while(x <= tot) c[x] = (c[x] + y) % MOD, x += (x & -x);
}
} tr1, tr2;
int query_sum(int r) { return ((LL)(r + 1) * tr1.query_sum(r) % MOD - tr2.query_sum(r) + MOD) % MOD; }
int query_sum(int l, int r) {
if(l == 0) return query_sum(r);
return (query_sum(r) - query_sum(l - 1) + MOD) % MOD;
}
void modify_add(int l, int r, int k) {
tr1.modify_add(r + 1, -k + MOD), tr1.modify_add(l, k);
tr2.modify_add(r + 1, -((LL)k * (r + 1) % MOD) + MOD), tr2.modify_add(l, (LL)k * l % MOD);
}
};
|
题目推荐
洛谷 P3374
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include <cstdio>
#include <cstring>
const int N = 5e5 + 5;
const int INF = 0x3f3f3f3f;
int a[N], dif[N], c[N];
int n, m;
inline int lowbit(int x) { return x & -x; }
void change(int x, int d) {
while(x <= n) {
c[x] += d;
x += lowbit(x);
}
}
int total(int x) {
int tot = 0;
while(x) {
tot += c[x];
x -= lowbit(x);
}
return tot;
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) c[i] = 0;
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
for(int i = 1; i <= n; i++) dif[i] = a[i] - a[i - 1];
for(int i = 1; i <= n; i++) change(i, dif[i]);
for(int i = 1; i <= m; i++) {
int type;
scanf("%d", &type);
if(type == 1) {
int l, r, k;
scanf("%d%d%d", &l, &r, &k);
change(l, k);
change(r + 1, -k);
} else {
int k;
scanf("%d", &k);
printf("%d\n", total(k));
}
}
return 0;
}
|
洛谷 P3368
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| #include <cstdio>
#include <cstring>
const int N = 5e5 + 5;
const int INF = 0x3f3f3f3f;
int c[N];
int n, m;
inline int lowbit(int x) { return x & -x; }
void change(int x, int d) {
while(x <= n) {
c[x] += d;
x += lowbit(x);
}
}
int total(int x) {
int tot = 0;
while(x) {
tot += c[x];
x -= lowbit(x);
}
return tot;
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) c[i] = 0;
for(int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
change(i, x);
}
for(int i = 1; i <= m; i++) {
int type, l, r;
scanf("%d%d%d", &type, &l, &r);
if(type == 1) change(l, r);
else printf("%d\n", total(r) - total(l - 1));
}
return 0;
}
|
