前置知识 字符串基础 倍增 基数排序 计数排序
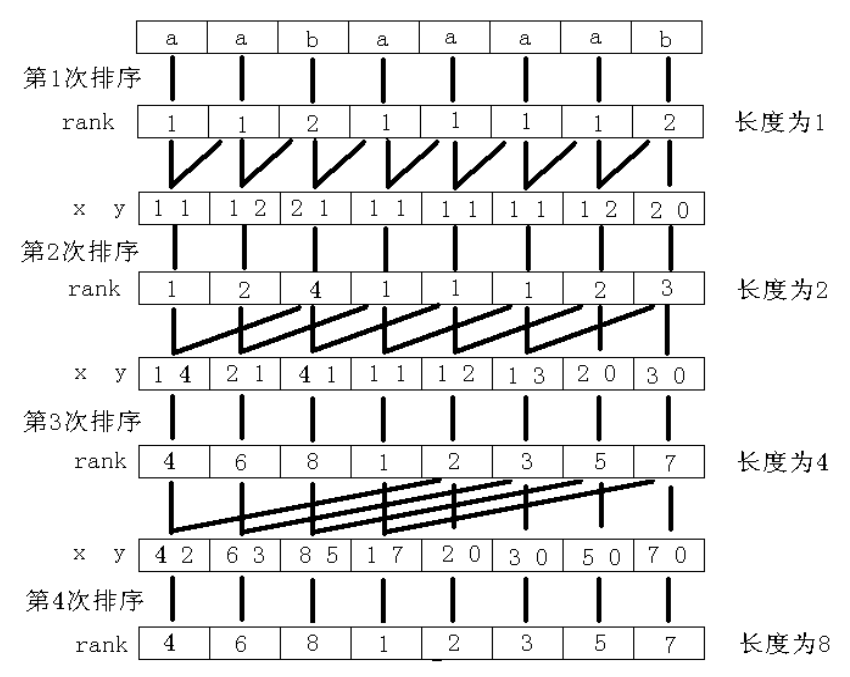
一些约定 字符串下标从 \(1\) 开始 字符串 \(t\) 长度为 \(len(t)\) 。特别的,字符串 \(s\) 长度为 \(n\) 本文中假设字符串只包含 小写字母 \(s[l..r]\) 表示 \(s_ls_{l+1}\ldots s_r\) 后缀 \(i\) 表示 \(s[i..n]\) 排名 \(i\) 后缀 表示所有后缀中字典序排名为 \(i\) 的那个的开始位置后缀数组 什么是后缀数组 后缀数组,顾名思义,就是存了后缀的数组。
其实后缀数组就是把所有后缀放在一起,然后按字典序排序。
盗一张 OI Wiki 的图。
后缀数组求法 求后缀数组的方法很多,比如说 \(O(n^2 \log n)\) 暴力,或者 \(O(n \log^2 n)\) 哈希,还有两种 \(O(n)\) 做法(SA-IS ,DC3 ,链接来自 OI Wiki 推荐),以及本文要讲的 倍增算法 。
算法思想 暴力的想法是,首先我们比较每个后缀 \(i\) 的第 \(1\) 个字符,然后比较第 \(2\) 个,然后第 \(3\) 个……一直到第 \(n\) 个。但这样是 \(O(n^2)\) 的。
那怎么优化它呢?别忘了我们的算法叫倍增啊!当我们对一个后缀 \(i\) 的前 \(w\) 位排完序时,后缀 \(i\) 的后面 \(w\) 位的顺序我们也是知道的!这时我们只需要对于后缀 \(i\) 中前 \(w\) 位的排名和后缀 \(i\) 中 \([w + 1 .. 2w]\) 位的排名进行双关键字排序,就可以得到后缀 \(i\) 中前 \(2w\) 位的排名啦!
再盗一张 OI Wiki 的图
具体实现 如果不想看 TLE 代码,可以直接移步到 优化实现 ,前面的内容是为优化实现作铺垫的。
变量约定 sa[i] — 排名 \(i\) 后缀的开始位置rk[i] — 后缀 \(i\) 的排名tp[i] — 即 temp,辅助数组,具体意思下面会说p — 辅助变量,具体意思下面会说sort 实现 现在我们可以写出代码啦!每次暴力更新第一、二关键字,用 sort 排序就好啦!
代码
代码来自 OI Wiki,变量大致是一样的(其实是我懒)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std;const int N = 1000010 ;char s[N];int n, w, sa[N], rk[N << 1 ], oldrk[N << 1 ];int main () int i, p; scanf ("%s" , s + 1 ); n = strlen (s + 1 ); for (i = 1 ; i <= n; ++i) sa[i] = i, rk[i] = s[i]; for (w = 1 ; w < n; w <<= 1 ) { sort (sa + 1 , sa + n + 1 , [](int x, int y) { return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y]; }); memcpy (oldrk, rk, sizeof (rk)); for (p = 0 , i = 1 ; i <= n; ++i) { if (oldrk[sa[i]] == oldrk[sa[i - 1 ]] && oldrk[sa[i] + w] == oldrk[sa[i - 1 ] + w]) { rk[sa[i]] = p; } else { rk[sa[i]] = ++p; } } } for (i = 1 ; i <= n; ++i) printf ("%d " , sa[i]); return 0 ; }
这样我们就可以 AC 了!
好打脸!
算啦,常数才不是我们要管的事,加 O2 不就能过了。\(O(n \log^2 n)\) 的了?我们的 优秀 算法怎么能允许这样的事出现?
基数排序实现 要让算法的复杂度为 \(O(n \log n)\) ,就要在排序上下功夫。\(O(n \log n)\) 。
代码
再次盗用 OI Wiki 的代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std;const int N = 1000010 ;char s[N];int n, sa[N], rk[N << 1 ], oldrk[N << 1 ], id[N], cnt[N];int main () int i, m, p, w; scanf ("%s" , s + 1 ); n = strlen (s + 1 ); m = max (n, 300 ); for (i = 1 ; i <= n; ++i) ++cnt[rk[i] = s[i]]; for (i = 1 ; i <= m; ++i) cnt[i] += cnt[i - 1 ]; for (i = n; i >= 1 ; --i) sa[cnt[rk[i]]--] = i; for (w = 1 ; w < n; w <<= 1 ) { memset (cnt, 0 , sizeof (cnt)); for (i = 1 ; i <= n; ++i) id[i] = sa[i]; for (i = 1 ; i <= n; ++i) ++cnt[rk[id[i] + w]]; for (i = 1 ; i <= m; ++i) cnt[i] += cnt[i - 1 ]; for (i = n; i >= 1 ; --i) sa[cnt[rk[id[i] + w]]--] = id[i]; memset (cnt, 0 , sizeof (cnt)); for (i = 1 ; i <= n; ++i) id[i] = sa[i]; for (i = 1 ; i <= n; ++i) ++cnt[rk[id[i]]]; for (i = 1 ; i <= m; ++i) cnt[i] += cnt[i - 1 ]; for (i = n; i >= 1 ; --i) sa[cnt[rk[id[i]]]--] = id[i]; memcpy (oldrk, rk, sizeof (rk)); for (p = 0 , i = 1 ; i <= n; ++i) { if (oldrk[sa[i]] == oldrk[sa[i - 1 ]] && oldrk[sa[i] + w] == oldrk[sa[i - 1 ] + w]) { rk[sa[i]] = p; } else { rk[sa[i]] = ++p; } } } for (i = 1 ; i <= n; ++i) printf ("%d " , sa[i]); return 0 ; }
这下终于可以 AC 了。
打脸第二次
为什么!明明复杂度是正确的!
优化实现 其实,基数排序中第二关键字可以不用计数排序,而是直接在存入时就排好序。
这里用我的代码详细讲解。(终于不是 OI Wiki 了)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 const int N = 1e6 + 5 ;char s[N];int n, m;int sa[N << 1 ], rk[N << 1 ], tot[N], tp[N];void Sort () for (int j = 0 ; j <= m; j++) tot[j] = 0 ; for (int j = 1 ; j <= n; j++) tot[rk[j]]++; for (int j = 0 ; j <= m; j++) tot[j] += tot[j - 1 ]; for (int j = n; j >= 1 ; j--) sa[tot[rk[tp[j]]]--] = tp[j]; } void SA () m = 'z' ; for (int j = 1 ; j <= n; j++) rk[j] = s[j], tp[j] = j; Sort (); for (int i = 1 , p = 0 ; p < n; i <<= 1 , m = p) { p = 0 ; for (int j = 1 ; j <= i; j++) tp[++p] = n - i + j; for (int j = 1 ; j <= n; j++) if (sa[j] > i) tp[++p] = sa[j] - i; Sort (); for (int j = 1 ; j <= n; j++) tp[j] = rk[j]; rk[sa[1 ]] = p = 1 ; for (int j = 2 ; j <= n; j++) rk[sa[j]] = ((tp[sa[j - 1 ]] == tp[sa[j]] && tp[sa[j - 1 ] + i] == tp[sa[j] + i]) ? p : ++p); } }
这一部分比较复杂,下面是详细讲解。
第一部分 1 2 3 4 5 6 7 void Sort () for (int j = 0 ; j <= m; j++) tot[j] = 0 ; for (int j = 1 ; j <= n; j++) tot[rk[j]]++; for (int j = 0 ; j <= m; j++) tot[j] += tot[j - 1 ]; for (int j = n; j >= 1 ; j--) sa[tot[rk[tp[j]]]--] = tp[j]; }
首先来看计数排序。计数排序的这里的作用是对第一关键字作稳定排序。下面分句看。
1 for (int j = 1 ; j <= n; j++) tot[rk[j]]++;
这里将所有的后缀 \(i\) 的排名记录到桶里。注意此时 rk 有可能相同,但排到最后肯定是不同的(因为长度都不同)。
1 for (int j = n; j >= 1 ; j--) sa[tot[rk[tp[j]]]--] = tp[j];
这里更新 sa,先说一下此时每个数组的意思。
tp[i] — 第二关键字排名为 \(i\) 的后缀的开始位置(至于为什么不直接记录后缀 \(i\) 的第二关键字,到后面就懂了)rk[i] — 上一轮排完后后缀 \(i\) 的排名,此处是后缀 \(i\) 的第一关键字。那么这句话就是枚举 第二关键字的排名 \(j\) ,那么 tp[j] 就是当前枚举的(第二关键字排名为 \(j\) 的)字符串的开头,又因为 sa[i] 表示排名 \(i\) 后缀的开头,所以这句话就是说:tot 作为这个字符串的排名,并将 tot 自减(tot 自减是计数排序的套路)。
注意到需要的是稳定排序,所以枚举是倒序的。
第二部分 1 2 for (int i = 1 , p = 0 ; p < n; i <<= 1 , m = p)
这里的 \(p\) 指的是已经排出的不同后缀的个数。
第三部分 1 2 3 4 p = 0 ; for (int j = 1 ; j <= i; j++) tp[++p] = n - i + j;for (int j = 1 ; j <= n; j++) if (sa[j] > i) tp[++p] = sa[j] - i;
这一部分是对第二关键字进行排序,也就是更新 tp。sa 就是原来的意思,tp 还是表示第二关键字排名为 \(i\) 的后缀的开始位置。
1 for (int j = 1 ; j <= i; j++) tp[++p] = n - i + j;
这里是将后缀 \(n - i + 1 .. n\) 进行排序,对于这些后缀,它们是没有第 \(i + 1 .. 2i\) 位的,所以要单独处理。
1 for (int j = 1 ; j <= n; j++) if (sa[j] > i) tp[++p] = sa[j] - i;
这一部分是对那些剩下的后缀(即后缀 \(1 .. n - i\) )排序,这里可以理解为我们在枚举 sa[j],即按第一次的排名枚举后缀。实际上,我们枚举的是剩下后缀的第 \(i+1\) 位,即第二关键字开始的位。所以这里就是说:\(j\) ,并将后缀 \(j - i\) 作为第 \(p\) 小的字符串,并将 \(p\) 自增。
第四部分 1 2 3 4 rk[sa[1 ]] = p = 1 ; for (int j = 2 ; j <= n; j++) rk[sa[j]] = ((tp[sa[j - 1 ]] == tp[sa[j]] && tp[sa[j - 1 ] + i] == tp[sa[j] + i]) ? p : ++p);
这里是对 \(rk\) 进行更新。此时各个数组的意义:
rk[i] — 这一轮后缀 \(i\) 的排名sa[i] — 这一轮排名 \(i\) 后缀开始的位置tp[i] — 上一轮后缀 \(i\) 的排名\(p\) — 已经排出的不同排名个这一部分就一起解释吧。
第 2 行将排名 \(1\) 后缀的排名和 \(p\) 置为 \(1\) 。(其实此时 \(p\) 还是计数器,不过计数完了就成了不同排名个数)\(rk\) 进行比较),不同将排名个数 \(p\) 加一。
压行实现 不讲。
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 const int N = 1e6 + 5 ;char s[N];int n, m;int sa[N << 1 ], rk[N << 1 ], tot[N], tp[N];void calcSA () m = 'z' ; for (int i = 0 , p = 0 ; p < n; i = (i ? i << 1 : 1 ), m = p) { if (i) { p = 0 ; for (int j = 1 ; j <= i; j++) tp[++p] = n - i + j; for (int j = 1 ; j <= n; j++) if (sa[j] > i) tp[++p] = sa[j] - i; } else for (int j = 1 ; j <= n; j++) rk[j] = s[j], tp[j] = j; for (int j = 0 ; j <= m; j++) tot[j] = 0 ; for (int j = 1 ; j <= n; j++) tot[rk[j]]++; for (int j = 0 ; j <= m; j++) tot[j] += tot[j - 1 ]; for (int j = n; j >= 1 ; j--) sa[tot[rk[tp[j]]]--] = tp[j]; if (!i) continue ; for (int j = 1 ; j <= n; j++) tp[j] = rk[j]; rk[sa[1 ]] = p = 1 ; for (int j = 2 ; j <= n; j++) rk[sa[j]] = ((tp[sa[j - 1 ]] == tp[sa[j]] && tp[sa[j - 1 ] + i] == tp[sa[j] + i]) ? p : ++p); } }
height 数组 定义 LCP 定义 \(lcp(s, t)\) 表示字符串 \(s\) 和 \(t\) 的最长公共前缀,也即最大的 \(i\) 满足 \(s[1..i]=t[1..i]\) 。
height 数组定义 \(height[i] = lcp(sa[i], sa[i - 1])\) ,即 \(height[i]\) 表示排名 \(i\) 和 \(i - 1\) 后缀的 LCP。
引理 引理:\(height[rk[i]] \ge height[rk[i - 1]] - 1\) ,即后缀 \(i\) 和排名前一位的后缀的LCP 不小于 后缀 \(i\) 排名前一位的和前两位的LCP \(-1\) 。
证明:(我不会证我懒,所以找了 OI Wiki 的证明 怎么又是 OI Wiki)
代码实现 1 2 3 4 5 6 7 8 9 void get_height () for (int i = 1 , k = 0 ; i <= n; i++) { if (rk[i] == 1 ) { ht[rk[i]] = 0 ; continue ; } if (k) k--; int j = sa[rk[i] - 1 ]; while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++; ht[rk[i]] = k; } }
参考资料 OI Wiki